この連載「【図解】Pythonプログラミングの始め方」では、大人気Pythonを扱う上で知っておきたい、基礎文法を図解を交えて分かりやすく解説していきます。Python学習の一助にしていただければ幸いです。
連載でとりあげる予定のコンテンツ一覧は次のとおりです。
連載2回目となる今回は、Pythonのデータ型について解説したいと思います。Pythonで扱うことができる「データの種類」について、そして各種データの操作を行うための「演算子」について解説します。
重要度:★★★★★
動的型式言語である、Pythonでは、変数定義時にデータ型宣言は必要ありませんし、数値の有効範囲により型(他言語でいうint, doubleなど)を選択する必要もありません。
このことは、Pythonプログラミングの難易度を下げる効果をもたらしますが、その一方でプログラマ自身はデータの属性を常に理解し適切な処理をする必要があります。
1. Pythonの「データ型」

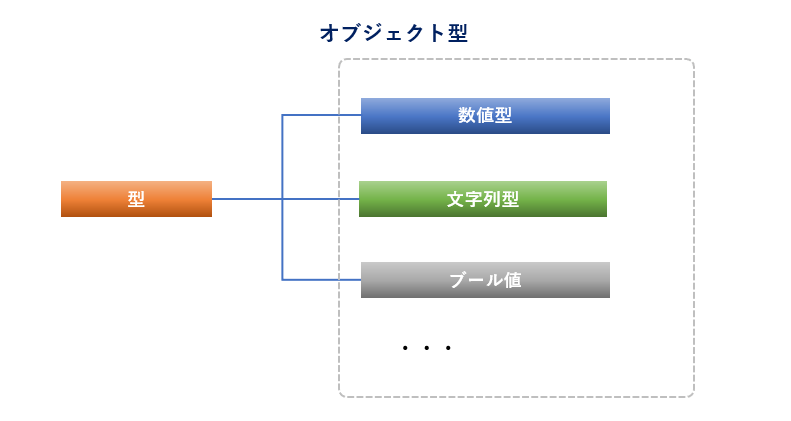
Pythonで使えるデータ型は、「数値型」「文字列型」「論理型」です。さらに、これらはすべてがオブジェクトなので、広義では「オブジェクト型」の一部となります。
一般的には、データ型といえば「数値型」「文字列型」「論理型」の3つあると考えればよいでしょう。
公式ドキュメントには、組込み型にはその他にも「シーケンス型」「イテレータ型」「ジェネレータ型」などにクラス分類されているようですが、本記事では、あくまでデータの型として扱い、データ構造の種類については別記事であらためて解説します。
3.10.7 Documentation >> The Python Standard Library >> Built-in Types
https://docs.python.org/3/library/stdtypes.html#built-in-types
それでは、次項より個々のデータ型について整理していきたいと思います。あわせて、関連する「演算子」についてもすべて紹介していきます。
2. 数値型

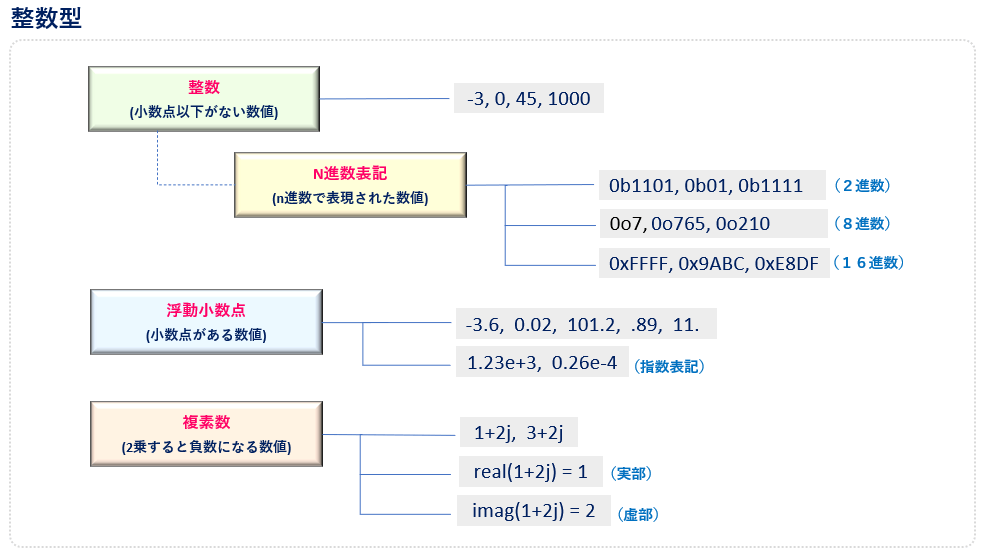
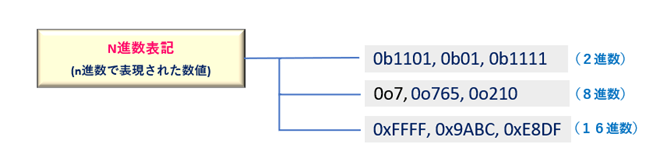
まずは数値型についてです。Pythonで表現できる数値型の種類は「整数」「浮動小数」「複素数」の3つに加え、整数の派生表現として「n進数表記」があります。(図2)
数値解析や行列演算といった用途に使われることの多いPythonでは、なんと複素数を標準で扱うことができます。
また、整数や浮動小数で扱うことができる数値範囲は、-10^10 から10^10といった長大(絶対値的に)なものから、0.1^(10)などきわめて小さい値まで対応できます。
さらに、Pythonは「動的型式言語」であるため、データの有効範囲を気にすることなく(あらかじめ、型宣言することなく)変数に代入・処理に使えます。
2.1 整数(Int)
整数は、小数点以下がない数値のことをいいます。負数や0も含めます。表現できる数値はメモリに格納できる範囲内で、長大な値を扱うことができます。また、アンダースコア(_)は、数値リテラルでは無視されるので、数値のグループ化することで可読性を高めることができます。(Python3.6以降)
Pythonは、整数オブジェクトを生成する標準関数に次の int()関数 を提供しています。他のデータ型から、整数に型変換(キャスト)することができます。
Init(x)関数
引数:x: 整数に変換するデータを設定する
戻り値: 整数オブジェクト
サンプルコードで確認してみます。
<List1>では、28桁の数値を扱っていますが、オバーフローすることなくそのまま使うことができるのがPythonを使うメリットの一つです。(B)また、整数の桁区切りとして、アンダースコア(_)を入れていますが、エラーは発生しません。(C)
print(5) # 5
print(0) # 0
print(-5) # -5
# 整数リテラルの長さには制限はない(メモリに格納出来うる範囲において)(B)
print(2147483647) # 2147483647
print(7922816251426433759354395033) # 7922816251426433759354395033
# アンダースコアを使って数値をグループ化することで分かりやすくすることができる (C)
print(100_000_000_000) # 100000000000》5
》0
》-5
整数リテラルの長さには制限はない(メモリに格納出来うる範囲において)(B)
》2147483647
》7922816251426433759354395033
アンダースコアを使って数値をグループ化することで分かりやすくすることができる (C)
》100000000000
2.1.1 算術演算子/代入算術演算子
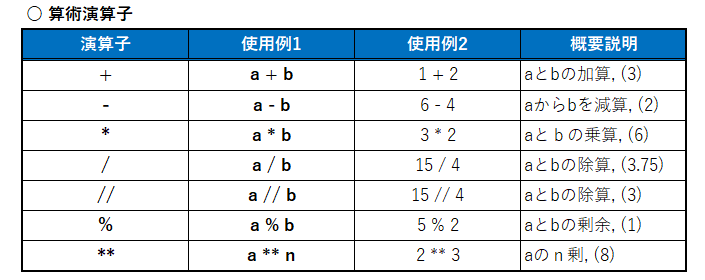
数値どうしの演算(整数に限らず)には、次の「算術演算子」を使います。全部で7種類で、べき乗(**)や、除算の商(//),余(%)も演算できます。(図4, List2)
また、Pythonは型混合(整数、浮動小数、複素数)の算術演算に対応しています。
型が異なる数値データの演算では、「広い方」の型に合わせて自動で型変換(キャスト)が行われます。
数値データは、整数<浮動小数<複素数 の順番にデータの有効範囲が広くなります。
算術演算子の使用例をコードで確認します。<List2>
print(100 + 10) # 110 ※➀ 加算
print(100 - 10) # 90 ※➁ 減算
print(100 * 10) # 1000 ※➂ 乗算
print(100 / 3) # 33.333333333333336 ※➃ 除算
print(100 // 3) # 33 ※➄ 商
print(100 % 3) # 1 ※➅ 剰余
print(2**3) # 8 ※➆ べき乗(累乗)算術演算子の実行結果
➀ 》110
➁ 》90
➂ 》1000
➃ 》33.333333333333336
➄ 》33
➅ 》1
➆ 》8
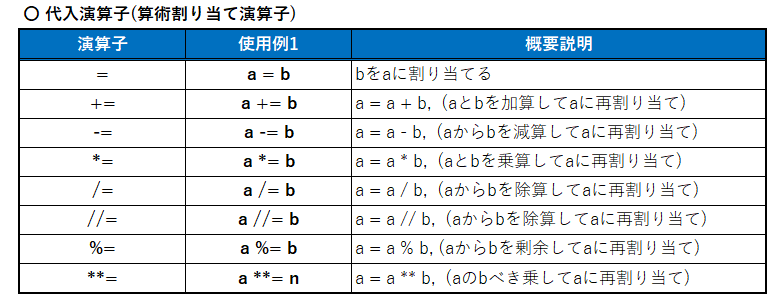
先の<List2>では、演算の結果をprint()関数で、直接コンソールへ出力していますが、通常のプログラムで行うような複雑な演算処理は、データを保存したストア領域(メモリ)に割り当てられた「変数」を介して、やり取り(アクセス)を行うことが普通です。
この変数へのデータの出し入れを、一つの式で、簡潔表現できる便利な演算子が「算術代入演算子」とよばれるものです。「算術演算子」に「=」記号を並べて表記し、同様に8種類が使えます。(図5)
「算術代入演算子」の使用例をコードで確認します。<List3>
# 代入演算子
num = 100
num *= 2 ;print(num) # 200 ➀. num = num * 2
num += 200 ;print(num) # 400 ➁. num = num + 200
num //= 4 ;print(num) # 100 ➂. num = num // 4算術代入演算子の実行結果
➀ 》200 # num = num * 2
➁ 》400 # num = num + 200
➂ 》100 # num = num // 4
整数については、以上です。引き続き、浮動小数(実数)について解説します。
2.2 n進数
整数は、通常10進数で表現されますが、ビット演算などをする場合は2進数(Binary)や16進数(Hexadecimal)で表現した方が便利な場合があります。
Pythonでは、2進数/8進数/16進数を扱うことができます。
n進数は、先頭に進数の「底」を示す識別子を付加することで、表現することができます。2進数は’0b___’, 8進数は‘0o__’, 16進数は’0x__’を付与します。
また、各進数に変換するための、標準関数( bin() / oct() / hec() )もあります。
<2進数> ‘0b___’
bin(x)関数
引数: x : 変換する数値を設定する
戻り値:整数(2進)オブジェクト
<8進数> ‘0o___’
oct(x)関数
引数: x : 変換する数値を設定する
戻り値:整数(8進)オブジェクト
<16進数> ‘0x___’
hex(x)関数
引数: x : 変換する数値を設定する
戻り値:整数(16進)オブジェクト
整数(2進数表記)オブジェクトに関連するメソッドを2つほど紹介します。
バイナリのビット数とビット列中の1の個数をカウントする機能を提供します。
整数オブジェクト(ビット表記).bit_length()
戻り値:符号と先頭の0を除いた、ビット数
整数オブジェクト(ビット表記).bit_count()
戻り値:ビット列の1の数
サンプルコードで確認してみます。
2/8/16進数をそれぞれ表記記号を付けて表現しています。また、➀➂➄のように<2.1.1項の算術演算子>で同じ基底どうしので演算することもできますし、➆のように基底が不揃いでも問題なく演算することができます。ただし、演算結果は、10進数に自動変換されますので、bin()関数 でバイナリに戻りしています。(➁➃➅)
#2進数(0b____)
print(0b0000) # 0
print(0b0101) # 5
print(0b1111) # 15
print(0b0001 + 0b1010) # 11 ※➀ 1 + 10
print(bin(0b0001 + 0b1010)) # 0b1011 ※➁ ➀の結果を2進数で出力
#8進数(0o____)
print(0o000) # 0
print(0o010) # 8
print(0o777) # 511
print(0o001 + 0o010) # 9 ※➂ 1 + 8
print(bin(0o001 + 0o010)) # 0b1001 ※➃ ➂の結果を2進数で出力
#16進数(0x____)
print(0x00) # 0
print(0x10) # 16
print(0xFF) # 255
print(0x01 + 0x10) # 17 ※➄ 1 + 16
print(bin(0x01 + 0x10)) # 0b10001 ※➅ ➄の結果を2進数で出力
#2,8,16進数間での演算
print(0b0001 + 0o010 + 0x10) # 25 ※➆ 1 + 8 + 162進数(0b__)
➀ 》11
➁ 》0b00
8進数(0o__)
➂ 》9
➃ 》0b1001
16進数(0x__)
➄ 》17
➅ 》0b10001
2, 8, 16進数での演算
➆ 》25
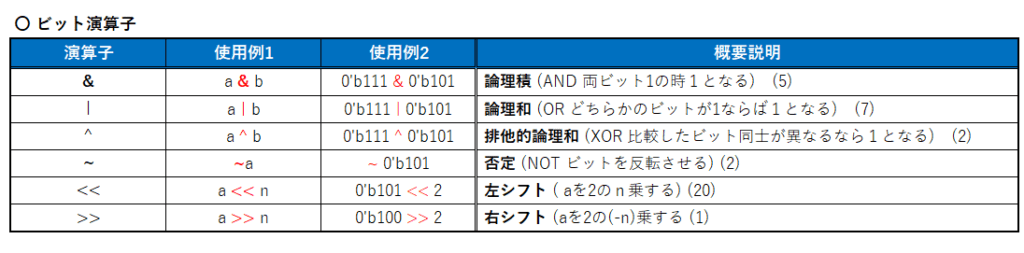
2.3.1 ビット演算子
ビット同士の演算には、下記の6種類の「ビット演算子」を使います。論理積(AND)、論理和(OR)から、ビットシフト(右/左)演算まで、用意されています。(図7)
ビット演算子を使う上で注意する点は、演算結果が整数(10進数)に自動で変換されてしまうことです。
例1. ➀~➃は、1bitどおしの演算結果です。演算結果は、10進数に自動変換されるので、この例では「bin()関数」で、2進数(バイナリ)表記に戻しています。
また、➄,➅のようにビット列どうしでの演算にも対応できますので、「&」「|」「^」を組合わせて、ビットマスク・抽出・反転などに応用ができます。詳細については、論理演算を扱う専門書籍に解説を譲ります。
print(bin(0b0 & 0b1)) #➀ 0b0
print(bin(0b1 & 0b1)) #➁ 0b1 # 1,2項ともに’0b1’の場合のみ’0b1’となる
print(bin(0b0 | 0b0)) #➂ 0b0 # 1,2項ともに’0b0’の場合のみ’0b0’となる
print(bin(0b0 | 0b1)) #➃ 0b1
num1 = 0b101010
num2 = 0b111000
print(bin(num1 & num2)) #➄ 0b101000
print(bin(num1 | num2)) #➅ 0b111010論理積
➀ 》0b0
➁ 》0b1
論理和
➂ 》0b0
➃ 》0b1
ビット列どうしの演算
➄ 》0b101000
➅ 》0b111010
例2. 続いて、ビットシフト演算子の使用例をしめします。シフトするたびに、2倍(左シフト)、1/2倍(右シフト)されます。
num3 = 0b0001
# <左シフト>
print(bin(num3 << 1)) #➀ 0b10 Dec(2) ※以降2のn乗倍となる
print(bin(num3 << 2)) #➁ 0b100 Dec(4)
print(bin(num3 << 3)) #➂ 0b1000 Dec(8)
num4 = 0b1000
# <右シフト>
print(bin(num4 >> 1)) #➃ 0b100 Dec(4) ※以降2の(-n)乗倍となる
print(bin(num4 >> 2)) #➄ 0b10 Dec(2)
print(bin(num4 >> 3)) #➅ 0b1 Dec(1)ビット演算子(左シフト)
➀ 》0b10
➁ 》0b100
➂ 》0b1000
ビット演算子(右シフト)
➃ 》0b100
➄ 》0b10
➅ 》0b1
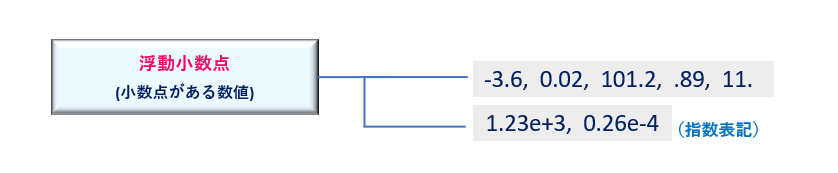
2.2 浮動小数(Float)
浮動小数点は、小数点以下を表現できる実数です。桁数が大きい場合は、指数表記(E)で表現でき、整数同様に、算術演算子が使えます、整数と浮動小数での演算では、浮動小数にキャスト(型変換)されます。(図8)
Pythonは、浮動小数オブジェクトを生成する標準関数として「float()関数」を提供しています。他のデータ型から、浮動小数に型変換(キャスト)することができます。
また、関連する2つのメソッドをあわせて紹介します。有限桁で表示できるかの判定と、浮動小数の16進数表記を戻す機能を提供します。
float(x)関数
引数:x:
戻り値:
<関連メソッド>
浮動小数オブジェクト.is_integer()メソッド
戻り値:浮動小数が有限であれば、True、そうでなければFalseを戻す
float.hex(x)関数
引数: x: 変換対象の浮動小数
戻り値: 16進数表記された浮動小数
サンプルコードで確認してみます。
例1.次は浮動小数点を表す例を紹介しています。小数点を含む正負の実数を表現することができます。また、整数部分や小数点以下の0は省略可能で、結果には0が自動的に追加されます。
整数同様に他言語で指定するような実数の取り扱いできる範囲指定・宣言(ビット指定)は不要です。(single, float など)
print(0.08) #➀ 0.08
print(98.5) #➁ 98.5
print(2343324234.200013134) #➂ 2343324234.200013
print(-3.5) #➃ -3.5 負数でも表現可
# "0 ""表記の省略
print(.123) #➄ 0.123 整数部の0を省略した場合
print(10.) #➅ 10.0 小数点以下の0を省略した場合➀ 》0.08
➁ 》98.5
➂ 》2343324234.200013
➃ 》-3.5
“0 “”表記の省略
➄ 》0.123 # 整数部の0を省略した場合
➅ 》10.0 # 小数点以下の0を省略した場合
例2. 次のように大きな桁数を表現する際には指数表記を使うことができます。指数表記の”e”はExponet(10を底とした指数)を表します。大文字”E”と記述しても同じです。
また、実数の演算結果が整数にキャストすることはありません。(➀)整数同様に”_”で区切り文字を使用しても結果に影響を与えません。(➃)
print(1.23e+7) #➀ 12300000.0 ※ 小数点以下は追加される
print(9.7e-4) #➁ 0.00097 ※ eの定数に負数を使うと(1/10)の累乗と同義
print(0e0) #➂ 0.0
print(3.14_15_93) #➃ 3.141593 # _による区切り文字も有効(整数同様)浮動小数の指数表記(e, E)
➀ 》12300000.0 # 小数点以下は追加される
➁ 》0.00097 # eの定数に負数を使うと(1/10)の累乗と同義
➂ 》0.0
➃ 》3.141593 # _による区切り文字も有効(整数同様)
例3.実数の計算例を紹介します。実数同士、また整数と実数といった計算ができますが全て結果は実数にキャストされます(➂,➃)。また、例外として整数同士の除算は実数になります。➄
print(10.3 + 0.5) # 10.8 ※➀ 実数 + 実数
print(10.3 - 0.5) # 9.8 ※➁ 実数 - 実数
print(100 * 0.2) # 20.0 ※➂ 整数 * 実数
print(1.08 * 100) # 108.0 ※➃ 実数 * 整数
print(100/2) # 50.0 ※➄ 整数 / 整数浮動小数の算術演算
➀ 》10.8 # 浮動小数 + 浮動小数
➁ 》9.8 # 浮動小数 – 浮動小数
➂ 》20.0 # 整数 * 浮動小数
➃ 》108.0 # 浮動小数 * 整数
➄ 》50.0 # 整数 / 整数
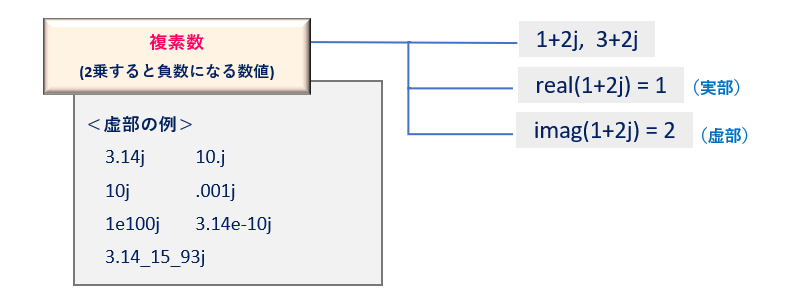
2.4 複素数 (Complex)
複素数は、実部と虚部を持ちそれぞれ浮動小数で表現されます。虚部は数値リテラルに‘j’もしくは、’J’を付けることで得られます(一般的に数学では‘i’で表す)。虚部を2乗すると負数になる性質をもつ特別な数値のことです。標準機能のとして、特別な宣言やモジュールのインポートなどをせずに、直ぐに使うことができます。
複素数(虚数)は、数値に’j’(J)を付加するだけで表現できますが、標準関数 complex() でも生成できます。
complex(re, im)関数
引数: re: 実部になる数値
引数: im: 虚部になる数値 オプション引数(省略するとゼロ)
戻り値: 複素数オブジェクト
複素数オブジェクトは、次のプロパティ(属性)で実部と虚部をそれぞれ取得することができます。
複素数オブジェクト.real
戻り値:実部
複素数オブジェクト.image
戻り値:虚部
サンプルコードで確認してみます。
例1. 次は、虚部を様々な形式で表現した例を示しています。➀のように、jの2乗で「-1」となりjが複素数(虚部)であることが分かります。浮動小数には整数以外にも、浮動小数<2.2項>を置くこともできます。
print(1j * 1j) # (-1+0j) ※➀ jの自乗は-1となる(定義そのもの)
print(10j) # 10j ※➁ 虚部のみ
print(2 + 3j) # (2+3j) ※➂ 実部+虚部
print(3.14j) # 3.14j ※➃ 実数を虚部にした場合
print(10.j) # 10j ※➄ 実数を虚部にした場合(.前後の0は省略可)
print(.001j) # 0.001j ※➅ 実数を虚部にした場合(.前後の0は省略可)
print(1e100j) # 1e+100j ※➆ 指数表記した虚部
print(1e-100j) # 1e-100j ※➇ 指数表記した虚部
print(3.14_15_93j) # 3.141593j ※➈ _による区切り文字も使用可能複素数のいろいろな表現方法
➀ 》(-1+0j) # jの自乗は-1となる(定義そのもの)
➁ 》10j # 虚部のみ
➂ 》(2+3j) # 実部+虚部
➃ 》3.14j # 実数を虚部にした場合
➄ 》10j # 実数を虚部にした場合(.前後の0は省略可)
➅ 》0.001j # 実数を虚部にした場合(.前後の0は省略可)
➆ 》1e+100j # 指数表記した虚部
➇ 》1e-100j # 指数表記した虚部
➈ 》3.141593j # _による区切り文字も使用可能
例2.複素数も<2.1.1項>の算術(代入)演算子が使えます。整数や浮動小数、複素数のどうしの演算ができます。
comp1 = 10 + 20j
comp2 = 30 + 40j
print(comp1 + comp2) # (40+60j) ※➀ 加算
print(comp1 - comp2) # (-20-20j) ※➁ 減算
print(comp1 * comp2) # (-500+1000j) ※➂ 乗算複素数どうしの演算
➀ 》(40+60j) # 複素数の加算
➁ 》(-20-20j) # 減算
➂ 》(-500+1000j) # 乗算
例3.複素数を生成する complex()関数 の使用例です。(➂➃) また、複素数オブジェクトには、real属性 と image属性 があり、それぞれ実部と虚部の数値を抽出することができます。
comp1 = 10 + 20j
print(comp1.real) # 10 ※➀ 複素数の実部
print(comp1.imag) # 20 ※➁ 複素数の虚部
#----------------------------------------------------------
comp2 = complex(3, 2)
print(comp2) # (3+2j) ※➂ 複素数の生成
comp3 = complex("1+2j") # (1+2j) ※➃ 複素数の生成(文字列による生成)
print(comp3)3. 文字列型

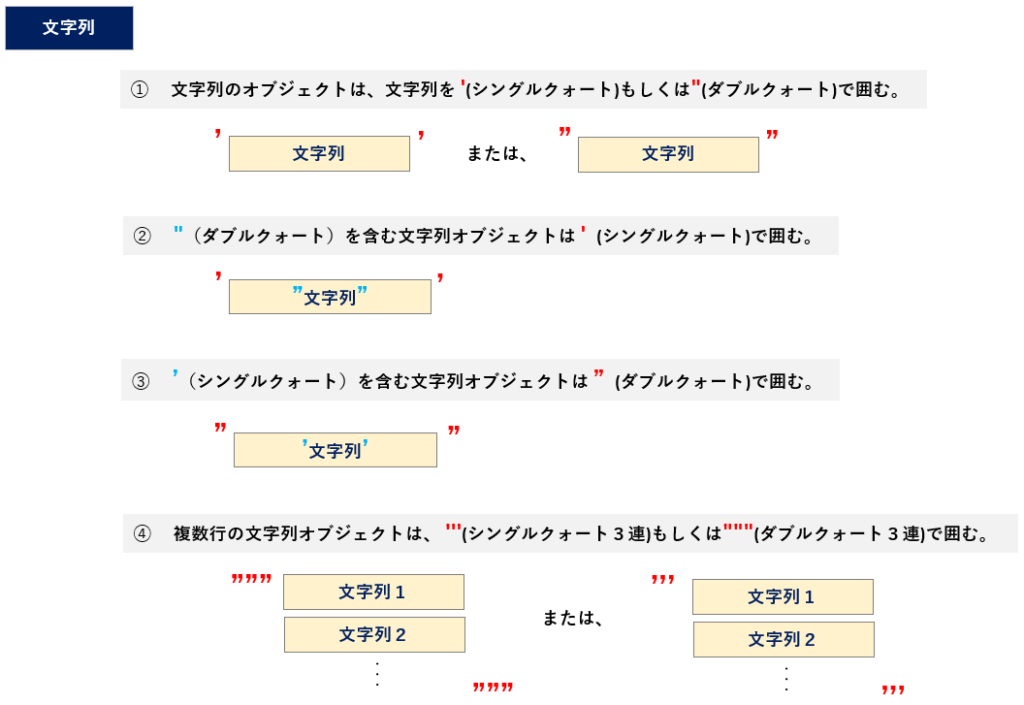
Pythonで文字列を表現するには、文字列を ‘(シングルクオーテーション) もしくは、“(ダブルクオーテーション) で囲むことで「文字列オブジェクト」として認識されます。その他の文字列に関連する書式をまとめると、以下のようになります。(図10)
<文字列リテラルの定義>
- ‘(シングルクォート) で囲む
- ”(ダブルクォート) で囲む
- “(ダブル)を含む文字列は、‘(シングル)で囲む
- ‘(シングル)を含む文字列は、“(ダブル)で囲む
- 複数行の文字列リテラルは、’’’(3連) で囲む、もしくは “””(3連) で囲む
- エスケープシーケンスで、文字列中に「改行」、「¥, ‘, “」文字を表現する
文字列中で、使うことができるエスケープシーケンスには、主として以下のような種類があります。その他のものは、公式サイトを参照してください。

サンプルコードで確認してみましょう。「‘」「“」で文字列オブジェクトをつくる基本型(A)と、複数行の文字列を「’‘’」で囲むこで、改行コードを含めて、そのまま文字列オブジェクトとして認識されます。(B) <List〇>
# 文字列型の基本的な使い方(A)
str1 = "Pythonの文字列型の解説_ダブルクォート"
print(str1) # >>Pythonの文字列型の解説_ダブルクォート
str2 = 'Pythonの文字列型の解説_シングルクォート'
print(str2) # >>Pythonの文字列型の解説_シングルクォート
str3 = 'Pythonの"文字列型"の解説'
print(str3) # >>Pythonの"文字列型"の解説
str4 = "Pythonの'文字列型'の解説"
print(str4) # >>Pythonの'文字列型'の解説
#-------------------------------------------------------------------------
# 複数行の文字列(B)
str5 = '''あいうえお
かきくけこ
さしすせそ
たちつてと
'''
str6 = """あいうえお
かきくけこ
さしすせそ
たちつてと
"""
print(str5)
print(str6)
# >>あいうえお
# >>かきくけこ
# >>さしすせそ
# >>たちつてと
#str6も同様3.1 文字列演算子
Pythonには、文字列を操作するための「文字列演算子」も提供されています。文字列どうしを連結する「+」と同じ文字(列)を繰り返す「*」演算子です。他の言語では、「&」などで連結することもありますが、Pythonでは「+」を使います。
また、文字列(オブジェクト)に、インデックスを指定して特定位置の文字(列)を取得することもできます。データ構造、リスト(List)のようにして扱うこともできます。(リストに関しては、こちらの記事を参照してください。)
それでは、サンプルコードで確認してみましょう。
例1. 次は、文字列を連結する例を示しています。連結できる文字列の数には上限はなく、「+」演算子でいくつでも連結できます。(➀,➁) また、文字列を格納した変数どうしも同様に連結が可能です。(➂,➃)
# 文字列の組み合わせ
print("ABC" + "_EFG") # ➀ ABC_EFG
print("ABC" + "_EFG" + "_HIG") # ➁ ABC_EFG_HIG
# 文字列と変数の組み合わせ
name = "Suzuki"
print("Hello_" + name) # ➂ Hello_Suzuki
print("Hello_" + name + "_Good Day") # ➃ Hello_Suzuki例2. 文字列と数値を連結する場合は、注意が必要です。数値演算子である「+」と競合して、コンパイルエラーが発生(TypeError)します。つまり、オブジェクト同士の型を統一する必要があります。文字列型として統一するには、数値を文字列にキャストする必要があり、今回は、「str()標準関数」を使って、文字列に型変換して連結するようにしています。
# 文字列と数字の組み合わせ(連結)
print("ABC" + 500) # ➀ TypeErrorが出力される
# TypeError: can only concatenate str (not "int") to str
print("ABC" + str(500)) # ➁ ABC500例3. 既定の文字(列)を指定回数分くりかえして連結する例です。「*」演算子にて対応します。次の例のように、「“文字(列)” * 回数」と記述します。文字(列), 記号など効率的に文字列リテラルを生成することができます。
# 文字列の繰り返し
print("A"*5) # ➀ AAAAA 文字
print("ABC"*3) # ➁ ABCABCABC 文字列
print('*'*10) # ➂ ********** 記号・・・
3.2 文字列オブジェクトの関連メソッド
Pythonに限らず、プログラミングでは文字列は大変重要なオブジェクトです。そのため、文字列オブジェクトの配下にはさまざまな「メソッド」がPythonの標準機能として提供されています。
文字列オブジェクトのメソッドについては、別記事で改めて解説しています。こちらを参照してください。
4. 論理型

比較演算子や論理演算子が成り立つ時は「True」(真)、成り立たない時は「False」(偽)の値をとります。主として、条件分岐<リンク>や繰り返しなど制御構文の「条件判定式」の戻り値として論理値を活用します。また、「True/False」はそれぞれ数値型では1/0で表され、算術演算子で演算も可能です。
基本的に、オブジェクトは“True”と判定されますが、以下のオブジェクトは“False”と判定されます。
<Falseと判定されるオブジェクト>
- None, 整数型のゼロ(0, 0.0, 0j…)
- 空リスト,タプル、辞書、コレクション(’’, [], (), {})
また、組込み関数の戻り値は、デフォルトでは偽(False/ゼロ)を返す仕様です。
4.1 比較演算子
リテラル(数値、文字列)の大小比較を行う演算子が「比較演算子」です。Pythonでは以下の6種類が用意されています。
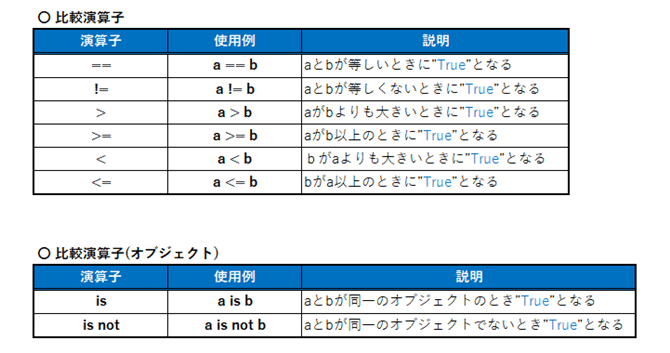
それでは、サンプルコードで確認してみましょう。
例1. 比較演算子の基本6種類の使用例を示しています。>= (以上)、<= (以下)は、“=”記号を右側につけて表記します。間にスペースなど間隔を挟むとエラーとなります。== (等号)、!= (不等号)も同様です。
num1 = 5; num2 = 5; num3 = 10;
#等号比較
print(num1 == num2) #➀ True (5 == 5)
print(num1 == num3) #➁ False (5 == 10)
print(num1 != num2) #➂ False (5 != 5)
print(num1 != num3) #➃ True (5 != 10)
#-------------------------------------------
#大なり比較
print(num1 > num2) #➄ False (5 > 5)
print(num3 > num1) #➅ True (10 > 5)
print(num1 >= num2) #➆ True (5 >= 5)
print(num3 >= num1) #➇ True (10 >= 5)
#-------------------------------------------
#小なり比較
print(num1 < num3) #➈ True (5 < 10)
print(num3 < num1) #➉ False (10 < 5)
print(num1 <= num3) #⑪ True (5 <= 10)
print(num3 <= num1) #⑫ False (10 <= 5)例2. 比較演算子の便利な書き方として、次のように2つの演算子を1つの式に結合してより数学的な記述スタイル表記しすることができます。これは、Pythonならではの書き方で、他言語ではこのような表記はできません。もちろん、Pythonも2回に分けて比較する書き方もできます。(というか、普通はそうします)
num = 20
print(10 <= num <= 25) #➀ True
num = 30
print(10 <= num <= 25) #➁ False
num = -5
print(-10 <= num <= 0) #➂ True
num = -15
print(-10 <= num <= 0) #➃ False4.2 論理演算子
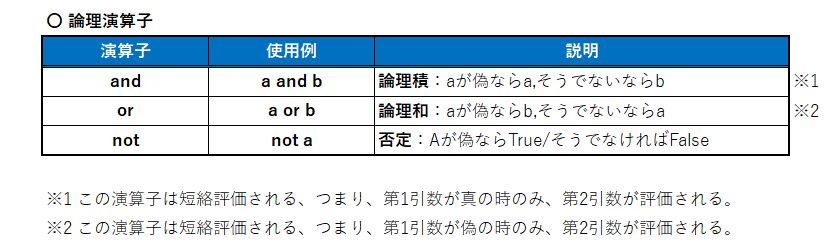
論理値(True/False)の演算は、次の「論演算子」を使います。「and」「or」「not」の3種類があります。
それでは、サンプルコードで確認してみましょう。
例1. 論理演算子の基本形の使い方です。
# <and/or/not の使い方>
print( False and False) #➀ False 両方がFlaseもしくは片方でもFalseならFalse
print( False or False) #➁ False 両方Falseの場合のみFalse
print( False and True) #➂ False
print( False or True) #➃ True 片方がTrueであればTrue
print( True and True) #➄ True 両方がTrueの場合のみTrue
print( True or True) #➅ True
# < notの使い方 >
print(not True) #➆ False 論理を反転する
print(not False) #➈ True例2. 演算子は、複数連結することがます。算術演算子とどうように、左から順番に処理されますが、「()」で優先度を変更できます。
# <3項の場合>
print( False and False and False) #➀ False
print( False or False or False) #➁ False
print( False and False and True) #➂ False
print( False or False or True) #➃ True例3. 4.1項の比較演算式を対象に、論理演算することもできます。
num = 80
print((num >= 50) and (num <= 100)) #➀ True 1項、2項ともTrueなので式全体がTrue
num = 110
print((num >= 50) and (num <= 100)) #➁ False 2項目がFalseなので式全体がFalse5. まとめ

最後に、この記事のまとめになります。
最後までお読み頂きありがとうございました。
次の記事では、文字列リテラルについて解説します。